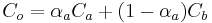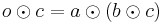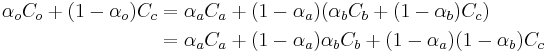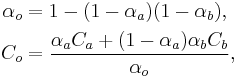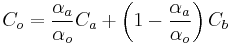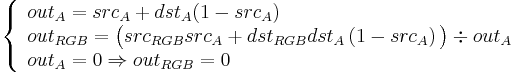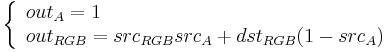Alpha compositing
In computer graphics, alpha compositing is the process of combining an image with a background to create the appearance of partial or full transparency. It is often useful to render image elements in separate passes, and then combine the resulting multiple 2D images into a single, final image in a process called compositing. For example, compositing is used extensively when combining computer rendered image elements with live footage.
In order to combine these image elements correctly, it is necessary to keep an associated matte for each element. This matte contains the coverage information—the shape of the geometry being drawn—making it possible to distinguish between parts of the image where the geometry was actually drawn and other parts of the image which are empty.
Contents |
Description
To store matte information, the concept of an alpha channel was introduced by Alvy Ray Smith in the late 1970s, and fully developed in a 1984 paper by Thomas Porter and Tom Duff.[1] In a 2D image element, which stores a color for each pixel, additional data is stored in the alpha channel with a value between 0 and 1. A value of 0 means that the pixel does not have any coverage information and is transparent; i.e. there was no color contribution from any geometry because the geometry did not overlap this pixel. A value of 1 means that the pixel is opaque because the geometry completely overlapped the pixel.
If an alpha channel is used in an image, it is common to also multiply the color by the alpha value, to save on additional multiplications during compositing. This is usually referred to as premultiplied alpha.
Assuming that the pixel color is expressed using straight (non-premultiplied) RGBA tuples, a pixel value of (0.0, 0.5, 0.0, 0.5) implies a pixel which has 50% of the maximum green intensity and 50% opacity. If the color were fully green, its RGBA would be (0, 1, 0, 0.5).
However, if this pixel uses premultiplied alpha, all of the RGB values (0, 1, 0) are multiplied by 0.5 and then the alpha is appended to the end to yield (0, 0.5, 0, 0.5). In this case, the 0.5 value for the G channel actually indicates 100% green intensity (with 50% opacity). For this reason, knowing whether a file uses premultiplied or straight alpha is essential to correctly process or composite it.
Premultiplied alpha has some practical advantages over normal alpha blending because premultiplied alpha blending is associative and linear interpolation gives better results, although premultiplication can cause a loss of precision and, in extreme cases, a noticeable loss of quality.
With the existence of an alpha channel, it is possible to express compositing image operations, using a compositing algebra. For example, given two image elements A and B, the most common compositing operation is to combine the images such that A appears in the foreground and B appears in the background. This can be expressed as A over B. In addition to over, Porter and Duff defined the compositing operators in, held out by (usually abbreviated out), atop, and xor (and the reverse operators rover, rin, rout, and ratop) from a consideration of choices in blending the colors of two pixels when their coverage is, conceptually, overlaid orthogonally:
The over operator is, in effect, the normal painting operation (see Painter's algorithm). The in operator is the alpha compositing equivalent of clipping.
As an example, the over operator can be accomplished by applying the following formula to each pixel value:
where 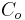 is the result of the operation,
is the result of the operation, 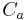 is the color of the pixel in element A,
is the color of the pixel in element A, 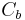 is the color of the pixel in element B, and
is the color of the pixel in element B, and 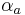 and
and 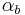 are the alpha of the pixels in elements A and B respectively. If it is assumed that all color values are premultiplied by their alpha values (
are the alpha of the pixels in elements A and B respectively. If it is assumed that all color values are premultiplied by their alpha values (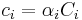 ), we can rewrite the equation for output color as:
), we can rewrite the equation for output color as:
and resulting alpha channel value is
However, this operation may not be appropriate for all applications, since it is not associative. The associative version of this operation is very similar; simply take the newly computed color value and divide it by its new alpha value, as follows:
Image editing applications that allow merging of layers generally prefer this second approach.
Analytical derivation of the over operator
Porter and Duff gave a geometric interpretation of the alpha compositing formula by studying orthogonal coverages. Another derivation of the formula, based on a physical reflectance/transmittance model, can be found in a 1981 paper by Bruce A. Wallace.[2]
A third approach is found by starting out with two very simple assumptions. For simplicity, we shall here use the shorthand notation  for representing the over operator.
for representing the over operator.
The first assumption is that in the case where the background is opaque (i.e. 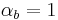 ), the over operator represents the convex combination of
), the over operator represents the convex combination of  and
and  :
:
The second assumption is that the operator must respect the associative rule:
Now, let us assume that  and
and  have variable transparencies, whereas
have variable transparencies, whereas  is opaque. We're interested in finding
is opaque. We're interested in finding
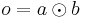 .
.
We know from the associative rule that the following must be true:
We know that  is opaque and thus follows that
is opaque and thus follows that  is opaque, so in the above equation, each
is opaque, so in the above equation, each  operator can be written as a convex combination:
operator can be written as a convex combination:
Hence we see that this represents an equation of the form 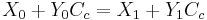 . By setting
. By setting 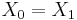 and
and 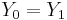 we get
we get
which means that we have analytically derived a formula for the output alpha and the output color of  .
.
An even more compact representation is given by noticing that 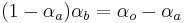 :
:
It is also interesting to note that the  operator fulfills all the requirements of a non-commutative monoid, where the identity element
operator fulfills all the requirements of a non-commutative monoid, where the identity element  is chosen such that
is chosen such that 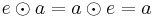 (i.e. the identity element can be any tuple
(i.e. the identity element can be any tuple 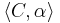 with
with 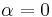 .)
.)
Alpha blending
Alpha blending is a convex combination of two colors allowing for transparency effects in computer graphics. The value of alpha in the color code ranges from 0.0 to 1.0, where 0.0 represents a fully transparent color, and 1.0 represents a fully opaque color. This corresponds to "SRC over DST" in Porter and Duff equations.
The value of the resulting color is given by:
If the destination background is opaque, then 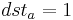 , and if you enter it to the upper equation:
, and if you enter it to the upper equation:
The alpha component may be used to blend to red, green and blue components equally, as in 32-bit RGBA, or, alternatively, there may be three alpha values specified corresponding to each of the primary colors for spectral color filtering.
Note that the RGB color may be premultiplied, hence saving the additional multiplication before RGB in the equation above. This can be a considerable saving in processing time given that images are often made up of millions of pixels.
Other transparency methods
Although used for similar purposes, transparent colors and image masks do not permit the smooth blending of the superimposed image pixels with those of the background (only whole image pixels or whole background pixels allowed).
A similar effect can be achieved with a 1-bit alpha channel, as found in the 16-bit RGBA Highcolor mode of the Truevision TGA image file format and related TARGA and AT-Vista/NU-Vista display adapters' Highcolor graphic mode. This mode devotes 5 bits for every primary RGB color (15-bit RGB) plus a remaining bit as the "alpha channel".
For some applications, a single alpha channel is not sufficient: a stained-glass window, for instance, requires a separate transparency channel for each RGB channel to model the red transparency, green transparency, and blue transparency. More alpha channels can be added for accurate spectral color filtration applications.
Applications
Alpha blending is used in a variety of applications. It is natively supported by most operating systems/GUIs for drawing windows (where applicable) or widgets:
- AmigaOS 4.1
- Android
- BeOS, magnussoft ZETA, Haiku
- Inferno
- Mac OS X, iOS
- MorphOS
- Plan 9
- QNX Neutrino
- RISC OS Adjust
- Syllable
- webOS
- Windows 2000 or later, CE, Mobile
- The XRender extension to the X Window System (this includes modern UNIX and Linux systems)
- GNOME 3.0
- Unity
- KDE (4.0 or later)
- Xfce
Other software may use alpha blended transparent elements in the GUI independently of OS provided APIs by precomposing elements in an off-screen memory buffer before displaying them. (Such as when displaying partially transparent composited elements in an embedded system which provides only a simple frame buffer.) Compositing software is used to combine images, and makes extensive use of alpha compositing techniques.
See also
- RGBA color space
- Digital compositing
- Transparency (graphic)
- Transparent color in palettes
- Image masks
- Portable Network Graphics
- Truevision TGA
- Magic Pink
- Texture splatting
- Alpha to coverage
References
- ^ Porter, Thomas; Tom Duff (1984). "Compositing Digital Images". Computer Graphics 18 (3): 253–259. doi:10.1145/800031.808606. ISBN 0897911385.
- ^ Wallace, Bruce (1981). "Merging and transformation of raster images for cartoon animation". SIGGRAPH Computer Graphics 15 (3): 253–262. doi:10.1145/800224.806813. ISBN 0897910451.
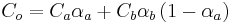
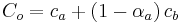
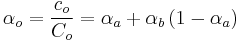
![C_o = \frac{1}{\alpha_o}\left[C_a \alpha_a %2B C_b \alpha_b \left(1 - \alpha_a\right)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/e9919ea79db8305dbdcfe98a5be66024.png)